Momentum is a measure of how much is required to stop a moving object. An object that is hard to stop has a large amount of momentum. An object that is easy to stop has a little momentum. Momentum depends on two things; mass and velocity. The equation for momentum is:

From this equation, a few things are obvious:
-The bigger something is, the more momentum it has.
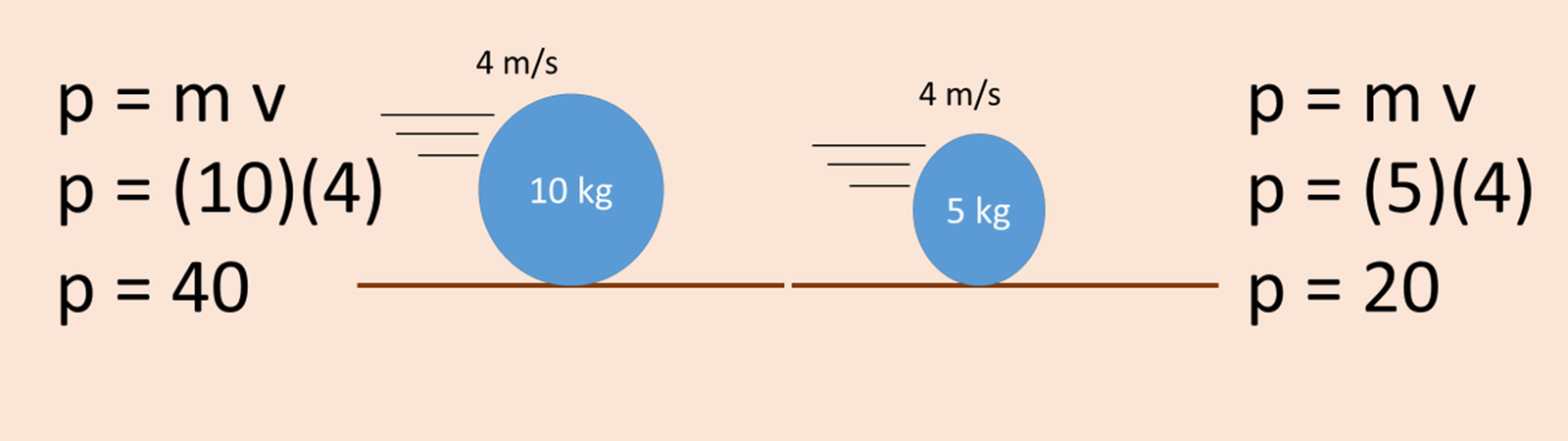
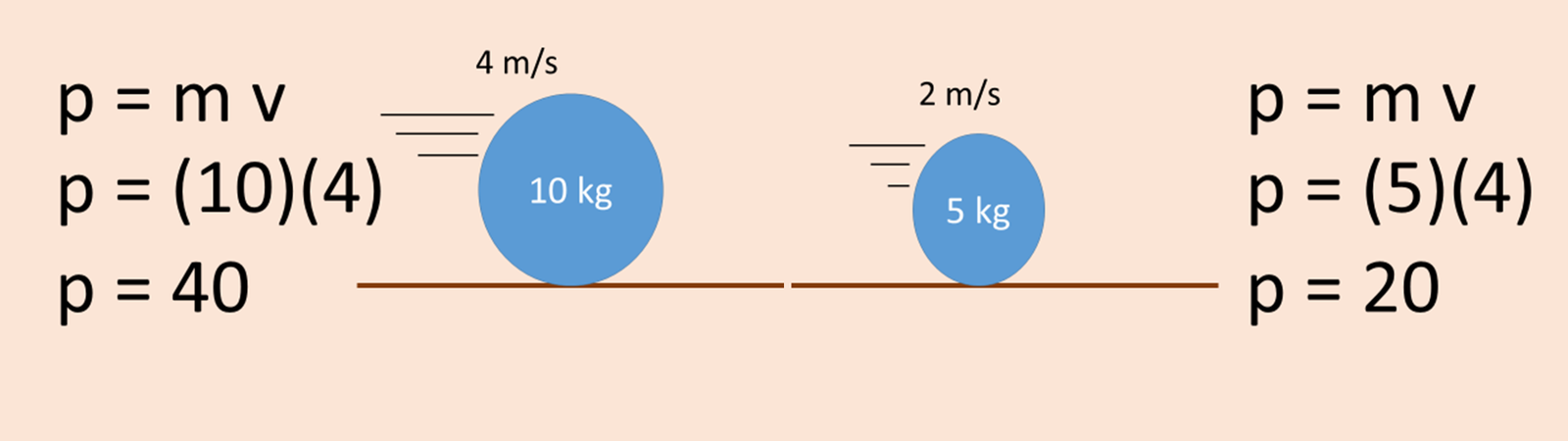
-The faster something is, the more momentum it has.
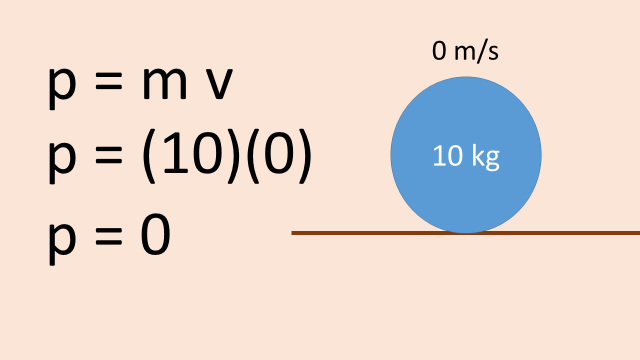
-If something is not moving, it has no momentum.
Momentum only changes if mass or velocity change. Most of the time, momentum changes because of velocity. It is far more common for an object to keep the same mass and change speed than to actually change mass while its moving. As long as an objects mass stays the same, the equation for change in momentum is:
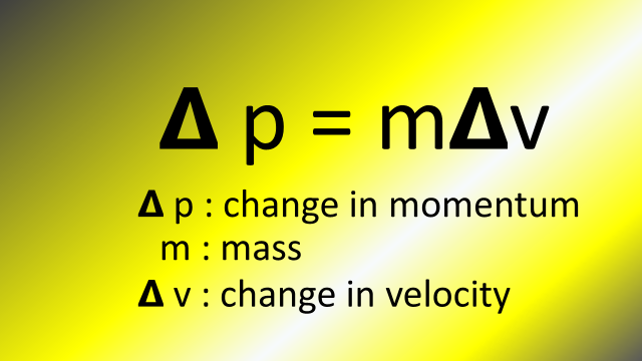
A change in momentum happens any time an object speeds up, slows down, or changes direction. Take a look at a few examples of calculating change in momentum:

In each of these examples, Buppa Head experienced a change in momentum. The change in his momentum is found by taking his mass and multiplying it by his change in velocity. Change in velocity is found by taking the velocity at the end of the event and subtracting the velocity at the beginning.
Imagine someone pushes on something for only a little while. Then another person pushes on the same thing with the same force, but for a longer time. The results would be different. I doesn�t just matter how much force you use; but also how long you use that force. The equation for Impulse is:

There are two ways to increase impulse. One is to apply a larger force. The other is to apply the force for longer. Both the strength of the force and the time the force is working are important. Consider the next two videos. In both videos an impulse is aplied to a bowling ball:
In the first video, the bowling ball is hit with a hammer. The hammer hits the bowling ball hard, but the hammer does not touch the ball for long. The force is large, but the change in time is small. In the second video, the bowling ball is hit with a rolled up piece of paper. The paper can�t hit the bowling ball very hard, but it pushes on the ball for a long time. The force is small, but the change in time is longer. In both videos, the bowling ball reaches about the same speed. This tells us that the impulse from the hammer and paper were about the same.
Impulse is something an object does. Change in momentum is what is done to an object. The two quantities are equal. Impulse equals change in momentum.

Using this equation we can see why some impacts are more dangerous than others. The way it works out, a large time of collision means a small force, but a small time of collision means a large force.
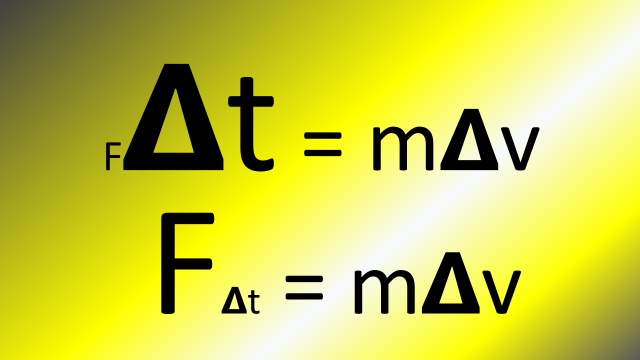
Take Buppa head for example. Buppa head runs into a brick wall, he comes to a stop very quickly. That means his time of collision is small. With a small time of collision there must have been larger force. When he ran into the haystack, the time that he took to come to a complete stop was longer. The longer time of collision meant a smaller force.
Play with the time of collision, and see what happens to his force.



Impulse = Change in Momentum
force x time of collision = mass x change in velocity
Whenever two objects collide, they exert a force on each other. The forces that they exert on each other, like all forces, obey Newton's third law. The forces are equal.
The force that object 1 exerts on object 2 is equal to the force that object 2 exerts on object 1. The two forces are equal in strength and opposite in direction. The difference in direction is shown by a negative sign when the situation is put into an equation.
The time that object 1 exerts a force is exactly the same as the time that object 2 exerts a force. It is impossible for one thing to touch another for longer than the other thing touches it.
Since force and time of contact are equal, the impulse that both exert on the other are equal and opposite.
We learned earlier that change in momentum is equal to impulse. This means that since impulse is equal and opposite, so is the change in momentum. However much momentum one object loses or gains, that is how much momentum the other object gains or loses. The change in momentums will be opposite; which means the same number but different directions. Watch this example:
As you can see from the video above; because we know that the change of momentum is equal and opposite, we can predict what happens after the collision. An important thing to keep track of in these collisions is the total momentum. The total momentum is what you get when you add the momentums of both objects together. The total momentum is important because it does not change. It is the same before the collision as after the collision. This is called conservation of momentum. Conservation of momentum is true for every collision. We can use conservation of momentum to solve a variety of problems involving two object collisions.
There are three main types of collisions: stick together collisions, bounce-off collisions, and explosions. In all three of these collisions, conservation of momentum can be used to predict what happens after the collision.
A bounce off collision is when two object run into each other and then separate from each other. There are two objects to keep track of before the collision and two objects to keep track of after the collision. If we know the mass and velocity of each object before the collision, we can calculate the total momentum. The total momentum will stay the same after the collision even though the momentum of each individual object changes. If we know one of the object�s velocity after the collision, we can predict the other object�s velocity. Here is the equation for bounce of collisions:

The left side of the equation is the total momentum before the collision. Since there are two objects before the collision, you find the momentum of those two things and then add them together. This gives you the total momentum. The total momentum after the collision is found the same way using the objects' new velocities after the collision.
This equation can be used to predict the velocity of one of one of the objects. For this to be possible, we have to know both velocities before the collision and one of the velocities after the collision. If so, we can find the missing velocity.
We will show two methods of solving two object collisions. The first method is to use the equation and solve for the missing variable. The second method is to use a table with mass, velocity, and momentum before and after the collision. There are rules for filling out the blanks in the table:
Here is are videos showing how to solve a bounce of collision problem using both ways:
A stick together collision is where two objects collide and then stick together. Before the collision, there are two objects. After the collision, there is one object. To find the total momentum before the collision, you need to add together the momentum of each object. After the collision, you can treat the two objects as if they were one object. The mass after the collision is equal to the mass of both objects added together. The momentum of this one object is equal to the total momenetum before the collision. The equaiton looks like this:

As long as we know the mass and velocity of both objects, we can calculate how fast they will move when stuck together after the collision.
Here is an example. It has been worked out by equaiton in the first video and by table in the second video.
An explosion collision is when there is one object at the begining and more than one object in the end. Many different events can fit this catagory:
In all these examples, the object or group of objects are all moving together in the beginning, but move seperately in the end. In all these exaples, the total momentum before is equal to the total momentum after. Before the collision, there is only one one mass and one velocity. After the collision, there are multiple pieces. If you add together the momentum of each of these pieces, the total momentum will be the same as the whole object before the explosion.
To keep things simple, lets use examples where there is one object that becomes two after the explosion. In this case, the equation is:
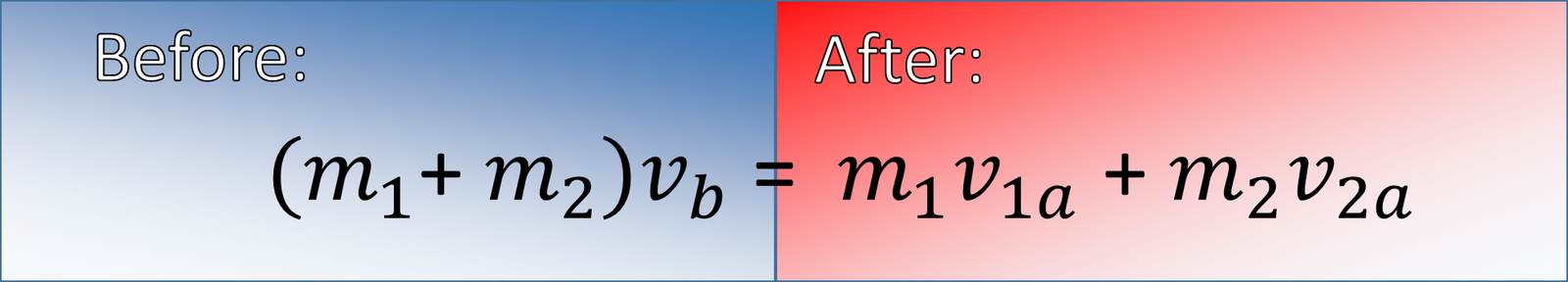
Often times with explosions, the object is not moving at first. When this is true, the total momentum before the explosion is 0.
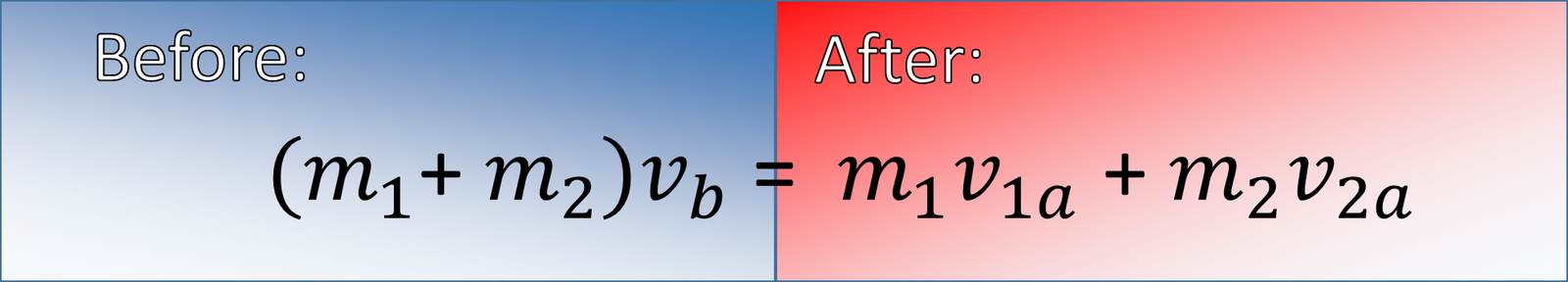
Notice that in this special case where the objects weren't moving before the explosion, the two objects will have momentum that is equal and opposite to each other.
when the objects are the same mass, they will move at the same speed but opposite direction:
When one object is larger, the momentum of both objects will be the same. However, the larger one will have a smaller velocity. It will move slower. This is because momentum depends not just on velocity, but also the mass. Each object's mass and velocity must multiply to give the same number. If the objects mass is large, the mass will need to multiply with a smaller velocity in order to have the same momentum as the smaller object. In other words, a small mass has a big change in velocity. A big mass has a small change in velocity.
This result is seen anytime two things push off each other. The larger object will move slowly the smaller object will move quickly. This is a result of conservation of momentum.
If we know the mass of both objects and one of the velocities after the explosion, we can calculate the other velocity. It has been worked out by equaiton in the first video and by table in the second video.