On the way up, Sargent Drop's gravitational potential energy is increasing. Since the elevator is increasing his energy, we say that the elevator is doing positive work. When he jumps off the building, his gravitational potential energy is turned to kinetic energy. Though the energy changed forms, the amount of Sargent Drop's energy stayed the same. No work is done. When he hits the cushion, he loses energy. Since it is taking energy away from him, the cushion is doing negative work on Sargent Drop.
Power = work / time
In Physics, Power refers to how fast work is done. In other words, power measures how fast energy is transferred from one thing to another. If we say that someone or something has a lot of power, it means that they can transfer their energy quickly to something else. Power is found by dividing the amount of work done by how long it took. Since work equals change in energy, you can also say that power equals the change in energy divided by time.
the unit for power is Watts. One Watt of power means that 1 Joule of work is done every 1 second.
So far, we've talked about how to know work is positive or negative. How do we find exactly how much work is done? We will look at 3 methods that can be used to find the amount of work:
Method #1 Force x Distance

Work equals Force times distance. The force in this equation only counts if it is in the same direction as the object is being moved. This equation accurately tells us the amount of work only when the direction of the force and the strength of the force both remain constant. Here is an example:
Mr. Stickman pushes his car. He pushes with a force of 500 N for 8 meters. It takes 40 seconds to push the car this distance.

Watch how this problem is solved in the video below:
If you need more help finding work from force, watch this video:
Method #2 From a Force vs Distance graph
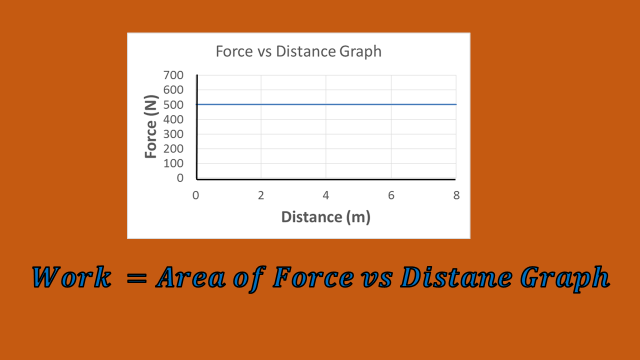
Work is equal to the area under a Force vs Time graph. This method allows us to find work in more complex situations, such as when force is not constant. Here is an example:
Sargent Drop is carried to the top of a building in an elevator. The force vs time graph shows the force the elevator uses to push Sargent Drop upward. How much work does the elevatior do on Sargent Drop.

Watch how this problem is solved in the video below:
If you need more help finding work from a force vs. time graph, watch this video:
Method #3 Work equals change in energy
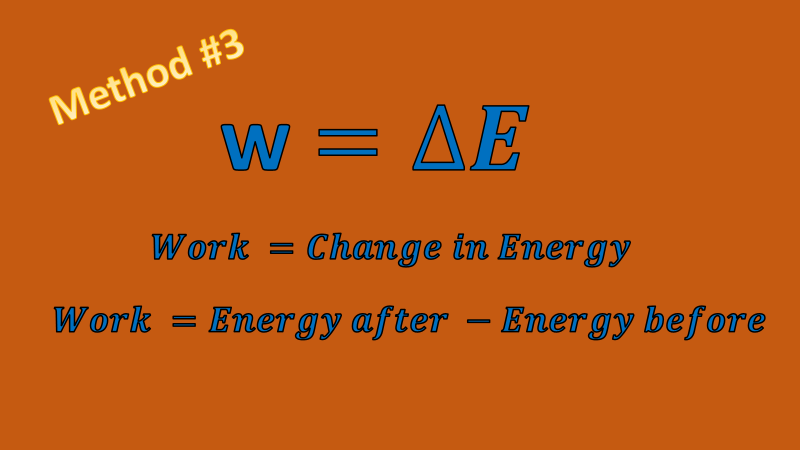
Doing work on something causes a change in energy for the object that is having work done to it. An object will gain exactly as much energy as the work that is done on it. We can use this fact to figure out how much work is done on something. Finding the change in energy is simple: Energy after the work - Energy after the work. Here is an example:
Kaw-Kaw Roach pushes his 0.2 kg ball up the top of a 2 meter high ramp. It takes 80 seconds to reach the top of the ramp.

Watch how this problem is solved in the video below:
If you need more help finding work from change in energy, watch this video:
Conservation of Energy
The total amount of energy does not change. Scientists have never observed energy being created or destroyed. Although the amount of energy never changes, energy does change. Energy changes from one form to another form. Energy also changes from one object to another object, or from one system (a group of objects) to another system. When one system loses energy, another system gains that same amount of energy. When the amount of one form of energy goes down, the amount of another form of energy goes up by the same amount. The total amount never changes.
Look at this example to see what happens to Sargent Drop's energy when he jumps off a cliff:
Notice that when he falls, his total energy will remain the same. However, the type of energy that he has changes. When he is at the top of the cliff, he has gravitational potential energy. As he falls, he loses gravitational potential energy. At the same time, he gains kinetic energy. The amount of gravitational energy that he loses is the same as the amount of kinetic energy he gains.
This change in energy effects his motion. As he loses height, he gains speed. The question is how much speed does he gain? We can find this information using the conservation of energy. Conservation of energy is the concept that the amount of energy in the beginning equals the amount of energy at the end (and anytime in between). We already have equations for gravitational energy and kinetic energy. As long as we have enough information, those equations will let us find velocity or height of an object. Look again at the example of Sargent drop jumping off the cliff. Let's say we know that the height of the cliff was 100 meters; and let's say we know that Sargent Drop's mass is 50 kg.
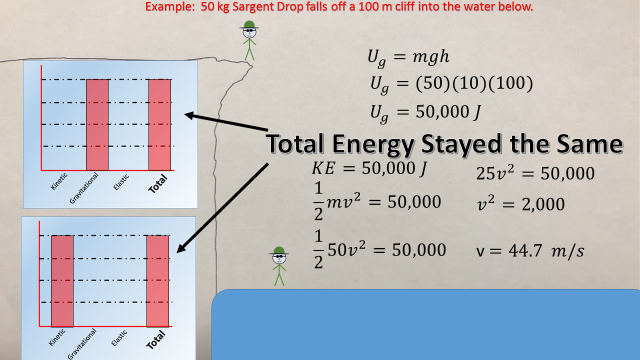
Because we know his height and mass, we can find out how much gravitational energy Sargent Drop had at the beginning (when he was at the top of the cliff). In the beginning, all of his mechanical energy was gravitational. He was not moving yet, so he could not have any kinetic energy. The amount of gravitational energy he had was also the amount of total mechanical energy he had. At the bottom, all his gravitational energy is turned into kinetic energy. Since we know how much energy he had at the top, we know how much kinetic energy he had at the bottom. The kinetic energy equation then lets us figure out what his velocity was.
Here is how the math works out:
Open Systems
If energy is conserved, why do things clearly run out of energy? For example:
As he falls using a parachutte, his velocity is limited. Because his velocity is limited, his kinetic energy is limited. As he falls, he loses gravitational energy. The amound of kinetic energy that he gains is limited because of the parachutte. As a result, his total energy is decreasing. What happens to this energy. Conservation of energy says that energy can't disappear. Whaere does the energy go?
Energy is leaving him and going into his surroundings. The parachute runs into the surrounding air particles causing the air molecules to move faster and causing him to move a little slower. As this happens, he is losing energy and the air is gaining energy. The amount of energy that he loses is equal to the amount of energy that the surroundings gain.
We can find out how much energy he lost by subtracting the energy he has at the end from how much energy he had at the beginning.
Look at this example: Sargent Drop, who is 50 kg, falls of a cliff that is 100 m tall. His parachutte limits his velocity to 10 m/s. How much energy does he lose during his fall? How much energy does the surroundings gain during his fall. Click on the picture to see how to solve the problem.

Sargent Drop starts his fall with 50,000 Joules of gravitational energy. He finishes his fall with 2,500 Joules of kinetic energy. This means that 47,500 Joules of energy were lost to the surroundings. The following are all true statements:
- Sargent Drop loses 47,500 Joules of energy
- His surroundings gain 47,500 Joules of energy
- Sargent Drop and his parachutte do 47,500 Joules of work on his surroundings
- His surroundings do -47,500 Joules of work on Sargent Drop
- The total energy of Sargent Drop + his surroundings stayed the same


