Let see if you understand distance and displacement. Play this game:







displacement: displacement
distance: distance
Won: 0
Lost: 0
Position and Time Data Table
In Physics, we study motion. There are ways to organize information about an object’s motion so that it is easier to see what is going on. Two of the most common ways are tables and graphs. A table looks like this:

position: position
A table keeps track of two or more pieces of information. The first column keeps track of time. The second column keeps track of what position the object was in at that time. Watch the video and see how the table is filled out.
As you can see in the video, every second that goes by, Mr. Stickman drops a red ball. At the end of his motion the picture looks like this:
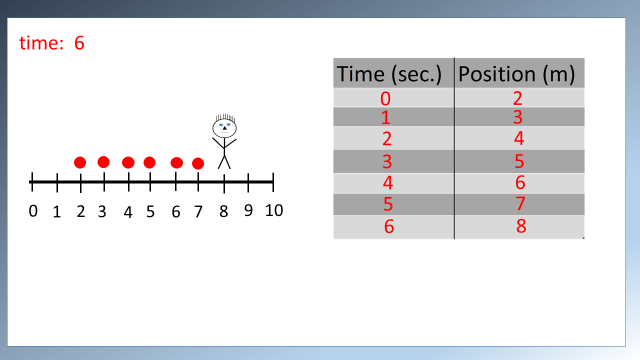
On the right, we have filled out a data table. The data table has time on the left and position on the right. By looking at this table, we can find out some information about Mr. Stickman’s motion. We can find out where it started. We can find out what direction he was going. We can find out his velocity. And, we can find out his displacement.
Starting point. The object’s starting point is the object’s position whenever time equals 0 seconds. At zero seconds, the position was 2.
Direction. The object’s position is increasing. This means that the object is moving away from the reference point (we usually call this ‘moving forward’). If the position numbers were getting smaller, it would mean that the object was coming toward the reference point (we usually call this ‘moving backward’). If the position numbers are not changing, that means the object is not moving.
Displacement. Displacement is how is a measure of how far an object is from where it started. Mr. Stickman started at 2 m and moved to 8 m. The way we can calculate displacement is final position – initial position. His final position is 8 m. His initial position is 2 m. 8 – 2 = 6 m . His displacement is 6 m.
Velocity. Velocity is a measure of how fast something is going and in what direction it is going in. To find velocity, look at any two rows of the table. Calculate how much position changes divided by how much time changes. If we look at the first and last row, position changes 6 m, time changes 6 s. 6/6 = 1. The velocity is 1 m/s.
Position vs Time Graph
Graphs are another way to visualize how an object is moving. It is easy to go from a data table to a graph. The values in the time column are graphed on the horizontal axis of the graph (sometimes called the x-axis). The values in the position column are graphed on the vertical axis of the graph (sometimes called the y-axis). Watch the following examples:
position: position
Notice as Mr. Stickman moves away, the graph line move upward. Whenever the line of a position vs. time graph moves upward, it means the object is moving away (forward).
Graphs can give us information about an object’s motion. From a graph, we can find out an object’s starting point, direction, velocity, and displacement. Take this graph from the above video as an example:
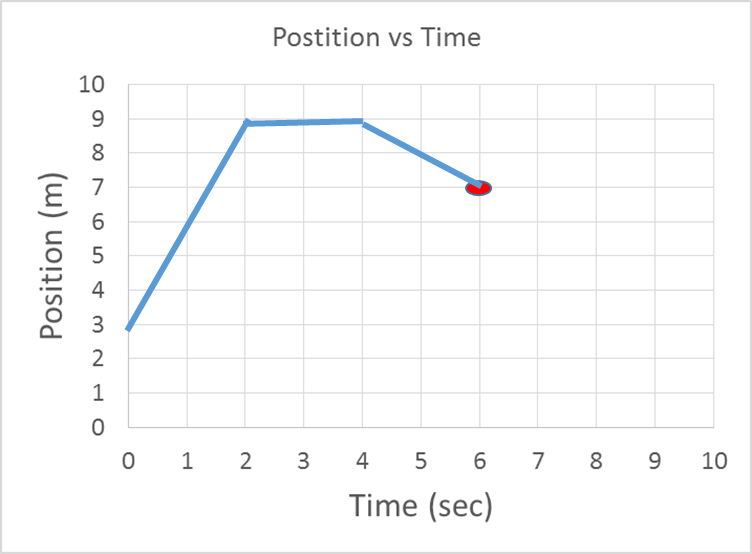
Starting point. Starting point is easy to find on a position vs. time graph. The position at zero seconds tells us the starting point. In math, this location is called the ‘y-intercept’ of the graph. In the graph above, the starting point is 3 meters.
Direction. The object is either moving away, not moving, or moving towards the reference point. If the graph’s line is sloping upward from left to right, the object is moving away (moving forward). If the graph’s line is sloping downward from left to right, the object is moving towards (moving backwards). If the graph line is flat, it means that the object is not moving. You can see from the graph above that the line slopes upward for the first two seconds. During this time, the object is moving forward. From 2 seconds to 4 seconds, the object does not move. We know that it does not move because the line is flat. From 4 to 6 seconds, the object is moving backwards. We know this because the line is sloping downward.
Displacement. Displacement can be found on this graph. Displacement = final position – initial position. The final position is 7. The initial position is 3. 7 – 3 = 4. The displacement is 4.
Velocity. Without doing any calculations, there is some information we know right away about the objects velocity. We know whether the velocity is positive or negative. When the line is sloping up, the velocity is positive. When the line is sloping down, the velocity is negative. We can also see whether the object is moving fast or slow. A steep line means fast. A not so steep line means slow.
There is a way to find out the exact value of the velocity. Velocity equals slope. If you find the slope of the line, you find the exact value of the velocity. As you may remember from Math class, slope is equal to rise over run. In other words, find how much the line goes up and then divide by how much the line goes across. Look at the graph again:
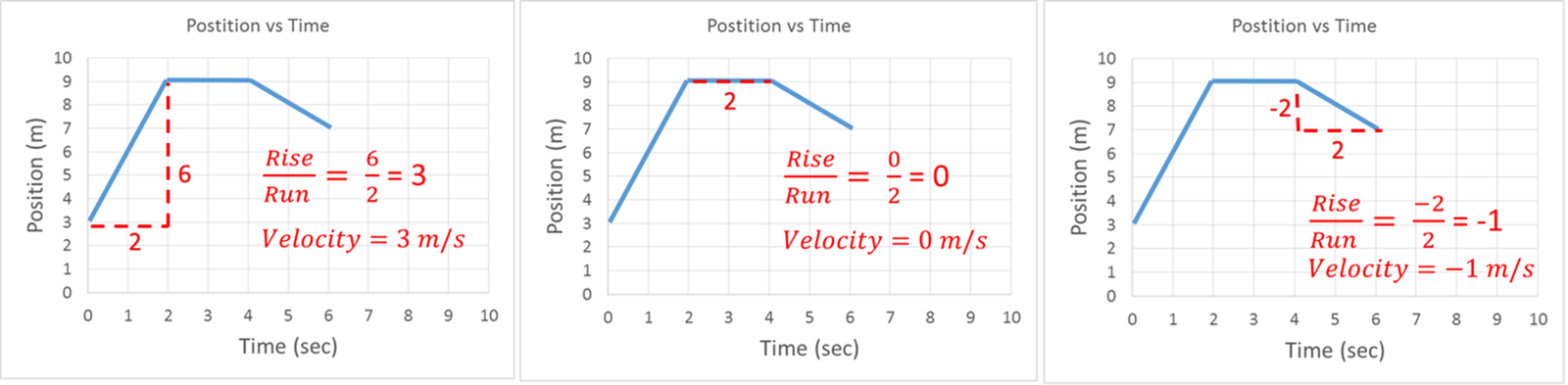
position: position
Each line segment of the graph has a different slope. This means there are three different velocities. For the first two seconds, the velocity is 3 m/s. For the next 2 seconds the velocity is 0 m/s. For the last two seconds, the velocity is -1 m/s. In each case, the velocity is found by dividing how much the line went up by how much the line went across.
Velocity vs Time Graph
So far, we have only looked at position vs. time graphs. In Physics, we will see many types of graphs. Another useful graph is the velocity vs. time graph. A velocity vs time graph shows how an object's velocity has changed over time.
Velocity measures how much position changes every second. If you measure the position of an object every second, you can easily see what the velocity is. It is equal to the change in position.

In this data table, you can see that the position increases by 3 meters every second. This tells us the velocity is 3 m/s. Since there is not always this nice of data, we need other ways to find velocity.
If you have a position vs. time graph, you can find the velocity by finding the slope of the graph line. Whatever the slope of the graph line is, that is also the velocity of the object for as long as that slope lasts. Here are some examples of going from a position vs. time graph to a velocity vs time graph.
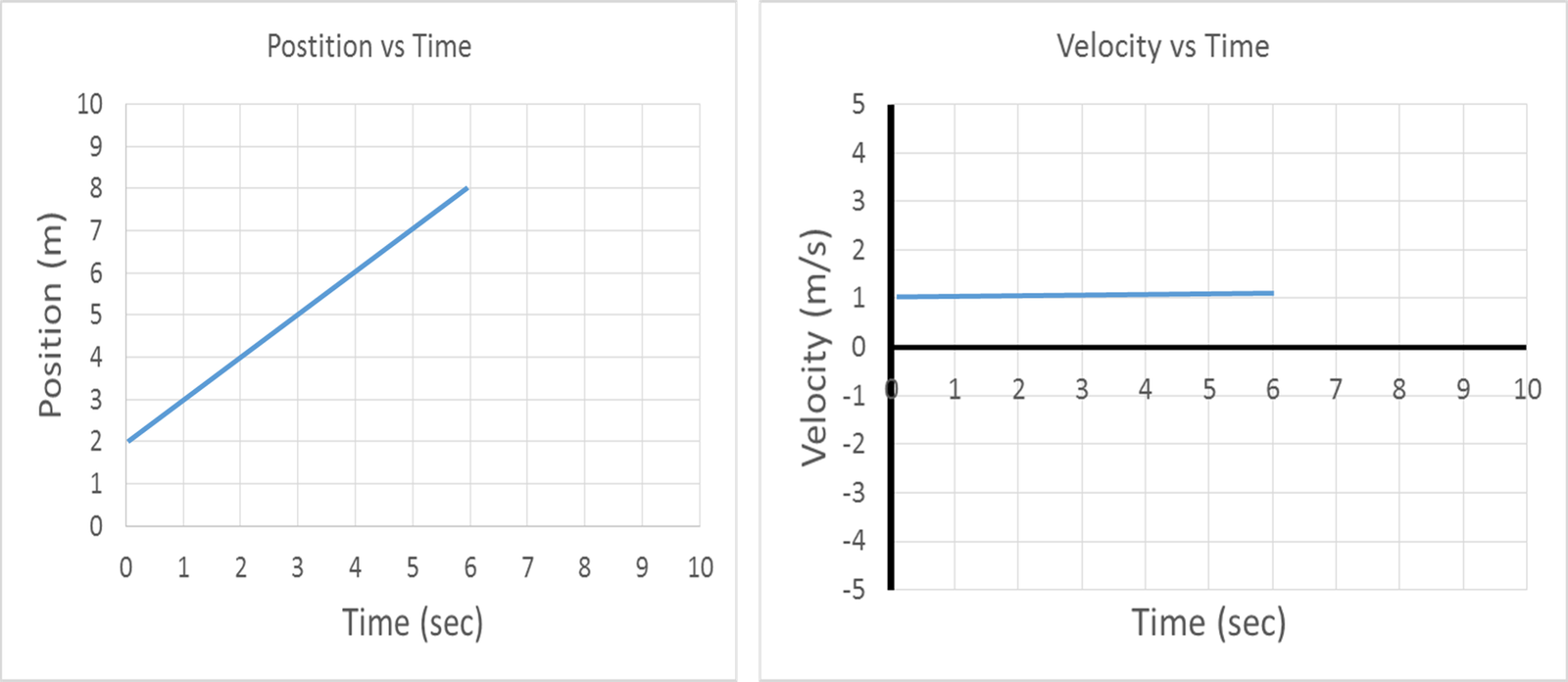
position: position
velocity: velocity
In the above example, the slope of the position vs. time graph is 1. Because the slope doesn’t change, we know that the velocity has not changed. The velocity has remained 1 m/s for the entire time. The velocity vs. time graph will always be a flat line when velocity is constant.
To help you understand position and velocity, play with the simulation below:
Graph Walker










Constant Velocity Equation
There is an equation that is useful for finding velocity:
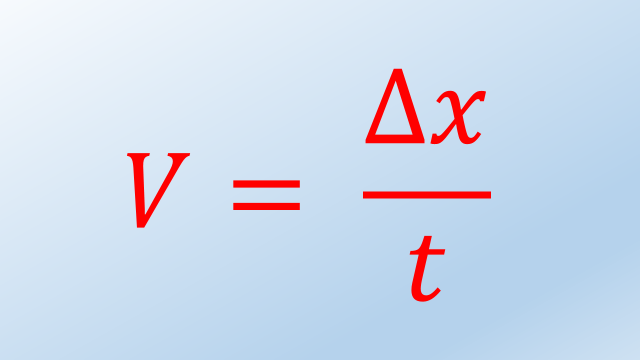
This equation only works when the velocity is not changing.
V stands for velocity.
Δx stands for displacement. The reason Δx is used for displacement is that displacement measures how much position has changed. 'Δ' means 'change'. 'x' means 'position' Δx is simply a measure of how much the position changes during the time period.
t stands for time. It is a measure of how much time has gone by during the time period you are measuring.
For instance, imagine you are measuring the motion of a toy car. You see the toy car go 4 meters in 5 seconds. As long as the car’s velocity is constant, you can use the equation to find the car’s velocity. The Δx is 4 meters because that is how much farther the car has gotten away from the reference point in that time. The t is 5 seconds because that is how much time changes while you are measuring the car’s motion. According to the equation the velocity is equal to 4 meters / 5 seconds = 0.8 m/s. If the car was going the same velocity for these 5 seconds, you can be sure that the velocity was 0.8 the entire time. However, if the car was speeding up or slowing down, what you actually found was the car’s average velocity.
In real life, numbers are often not very neat. Let’s say you measure a toy car’s motion and find the following information:
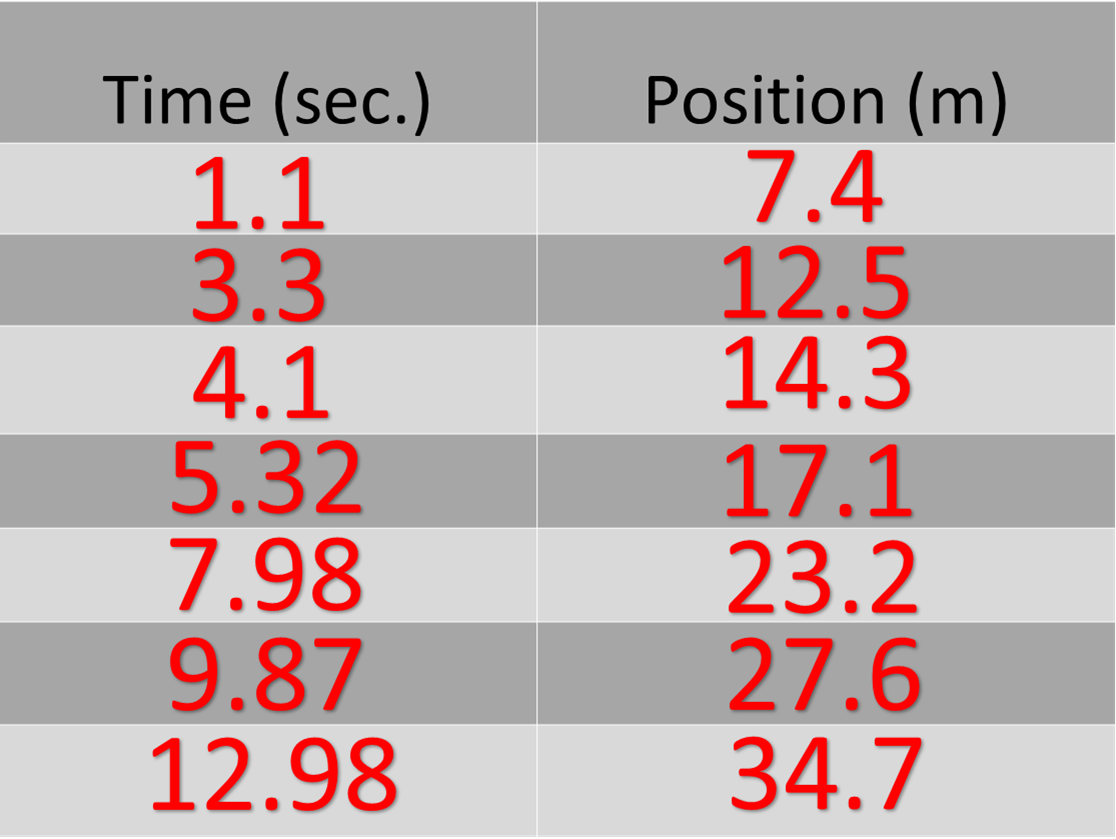
We can still find the velocity by using the equation. We need to find Δx. Δx the displacement. The displacement is found by seeing how much the positon has changed during this time:
Δx = Final position – initial position
Δx = 34.7 – 7.4
Δx = 27.3
We need to find t. The change in time is also final time – initial time = 12.98 – 1.1 = 11.88. According to the equation, v = Δx/t. Putting in the numbers we have found:
v = 27.3 / 11.88 = 2.3.
The velocity is 2.3 m/s.
In some questions, you are trying to find velocity. However, sometimes you need to find time or displacement. This equation can be used to find velocity, displacement, or time. The only requirement is that two of the three quantities are known. If so, we can find the missing value. To find displacement or time, the equation will first be rearranged.
To find displacement, rearrange the equation like this:
To find time, rearrange the equation like this:
Displacement from Velocity Graphs
Velocity graphs can be used to find distance and displacement. Displacement is equal to the area between the graph line and the graph’s horizontal axis.
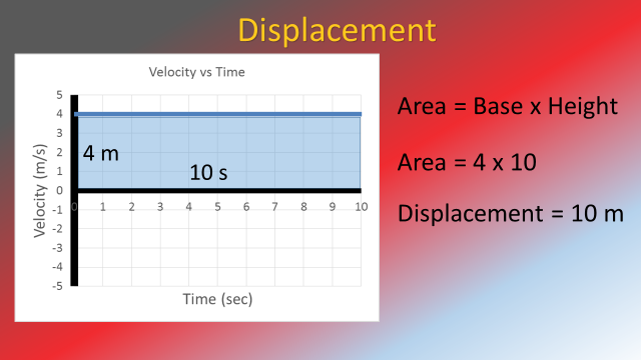
velocity: velocity
base: length of the graph's time access.
height: height of graph's velocity axis.
Play this game to see how well you know constant velocity: