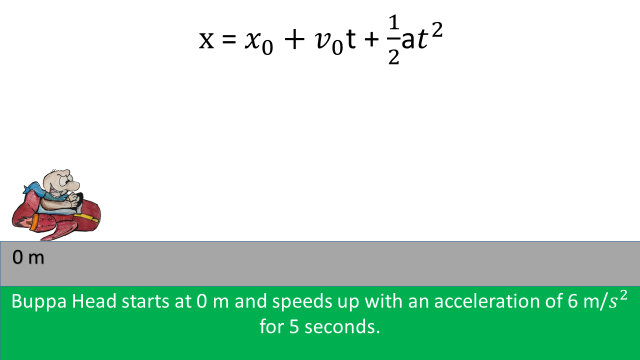Acceleration
What is Acceleration?
Four Types of Motion
Position Graphs With Acceleration
Velocity Graphs With Acceleration
Acceleration Equations
What is Acceleration
Not all motion is constant. Motion changes. When motion changes, there is acceleration. Acceleration is a measure of how much velocity changes. It is found by this equation:
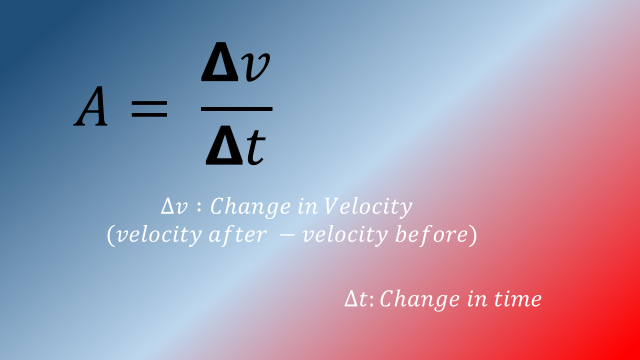
velocity before: velocity before
velocity after: velocity after
change in time: change in time
For example: a car speeds up from 10 m/s to 30 m/s in 8 seconds. The car's acceleration would be:
A = Δv/Δt
Δv = 30 - 10 = 20 m/s. Δt = 8 seconds
A = 20/8 = 2.5 m/s²
the acceleration would be 2.5 m/s²
Acceleration happens whenever an object:
- Speeds up
- Slows down
- Changes Direction
Acceleration: Acceleration
Notice that in the last example, acceleration was negative even though the car did not slow down. A positive acceleration does not always mean speeding up. A negative acceleration does not always mean slowing down.
What a positive acceleration always means is that the velocity is changing in a negative way.
This is confusing for many Physics students. We will now show several examples that will hopefully demonstrate positive and negative acceleration.
Four types of motions
We will look at four types of motion:
- Moving forward and speeding up
- Moving forward and slowing down
- Moving backward and speeding up
- Moving backward and slowing down
Moving forward and speeding up:

Position: Position
Velocity: Velocity
Acceleration: Acceleration
In this situation, we define the rightward direction to be positive and the leftward direction to be negative. By looking at how the position changes each second, we find the velocity. By looking at how the velocity changes each second, we find the acceleration. The velocity is increasing by a positive number. For this reason, the acceleration is positive.
Moving forward and slowing down:

Position: Position
Velocity: Velocity
Acceleration: Acceleration
In this situation, we defined the up direction to be positive and the downward direction to be negative. By looking at how the position changes each second, we find the velocity. By looking at how the velocity changes each second, we find the acceleration. The acceleration is negatvie, not because the object is slowing down, but because the velocity is increasing by a negative number.
Moving backward and speeding up:
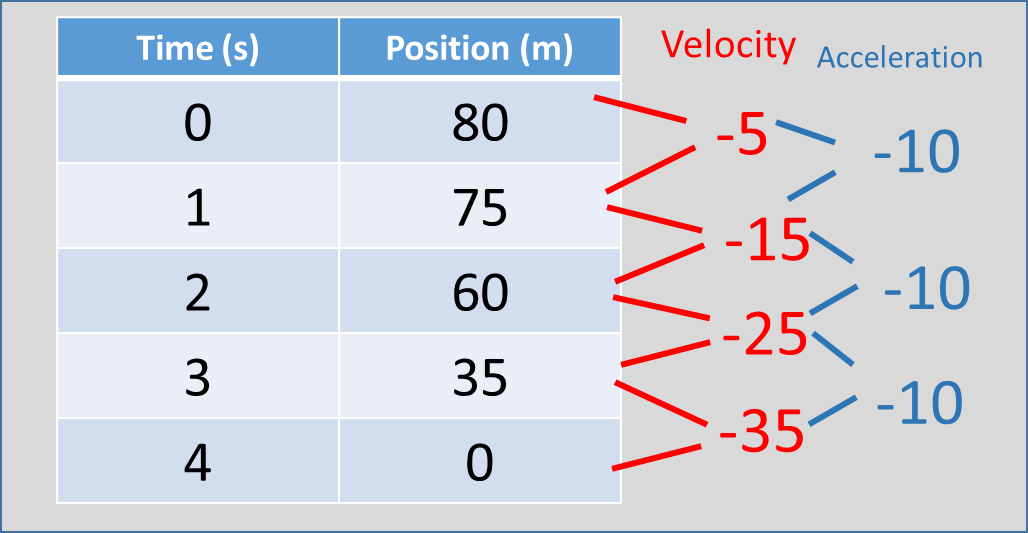
Position: Position
Velocity: Velocity
Acceleration: Acceleration
In this situation, we defined the up direction to be positive and the downward direction to be negative. The object is speeding up in the negative direction. Does this make the acceleration positive or negative? By looking at how the position changes each second, we find the velocity. By looking at how the velocity changes each second, we find the acceleration. Despite the object speeding up, the acceleration is negative. This is because the velocity is increasing by a negative number.
Moving backward and slowing down:

Position: Position
Velocity: Velocity
Acceleration: Acceleration
In this situation, we defined the up direction to be positive and the downward direction to be negative. The object is moving backward and slowing down. Does this mean that the acceleration is negative? By looking at how the position changes each second, we find the velocity. By looking at how the velocity changes each second, we find the acceleration. The acceleration is actually positive. This is because the velocity is increasing by a negative number.
Position Graphs with Acceleration
The affect of acceleration is seen on graphs of an object's motion. With position vs. time graphs, the rule is this: a curl down means negative acceleraton, a curl up means positive acceleration. If the line is straight, acceleration is zero. Here are some examples. Click on a graph to see an explanation of how acceleration affects the shape of the graph.
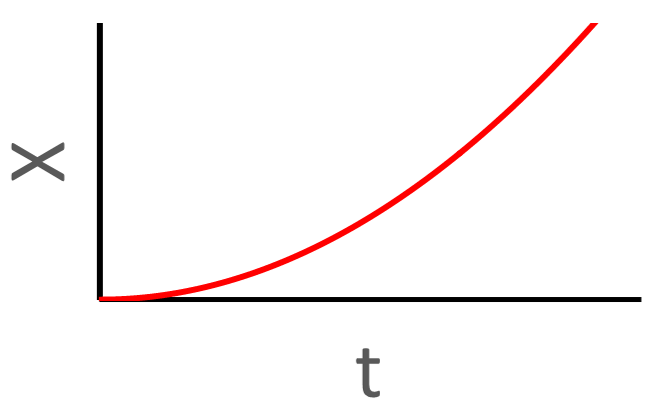
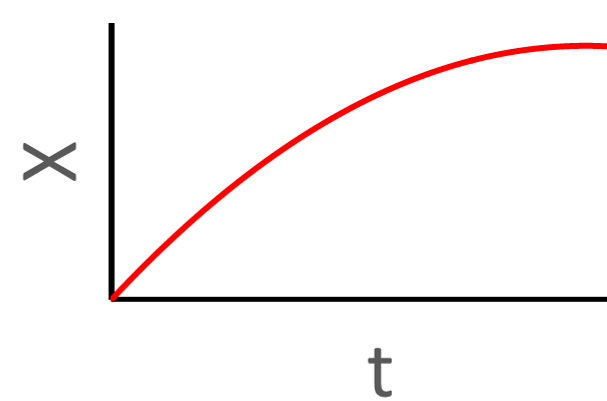
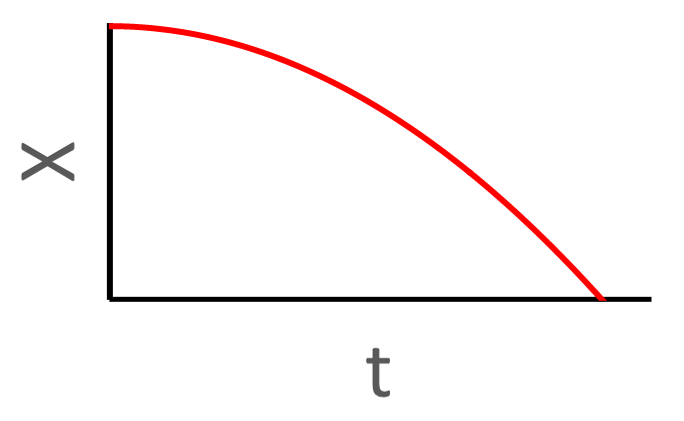
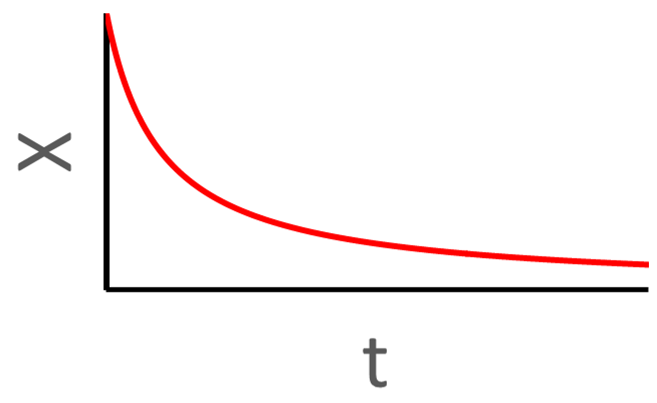

Click on a graph to see an explanation.
Velocity Graphs with Acceleration
With velocity vs. time graphs, a slope up means positive acceleration. A slope downward from left to right means a negative acceleration. You can tell whether the object is moving forward or backwards by where the graph line is. If the graph line is above the zero line, the velocity is positive and the object is moving forward. If the graph line is below the zero line, the velocity is negative and the object is moving backward. You can also tell whether the object is speeding up or slowing down. When you read the graph from left to right, if the graph line gets farther from zero, the object is speeding up. If the graphline is getting closer to zero, the object is slowing down.
Click on a graph to see an explanation what is happening in each graph:
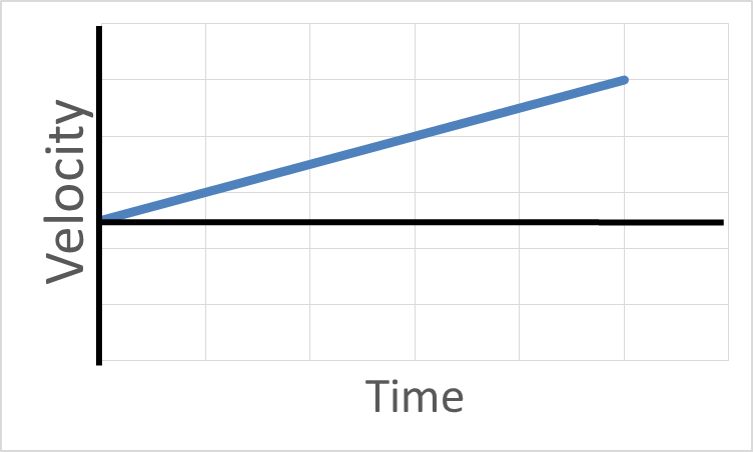
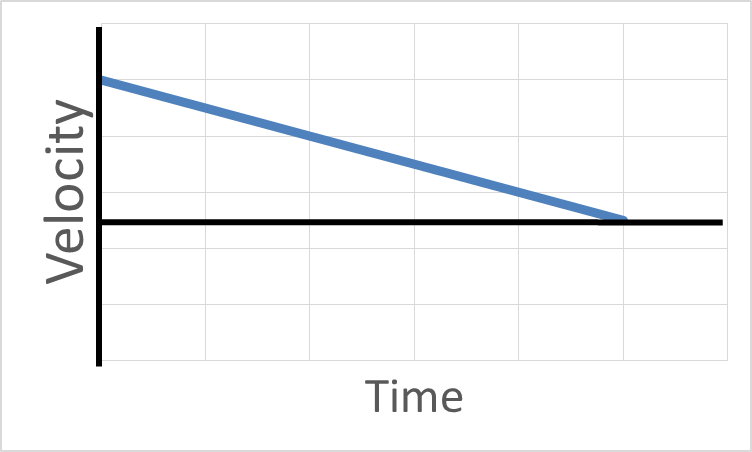
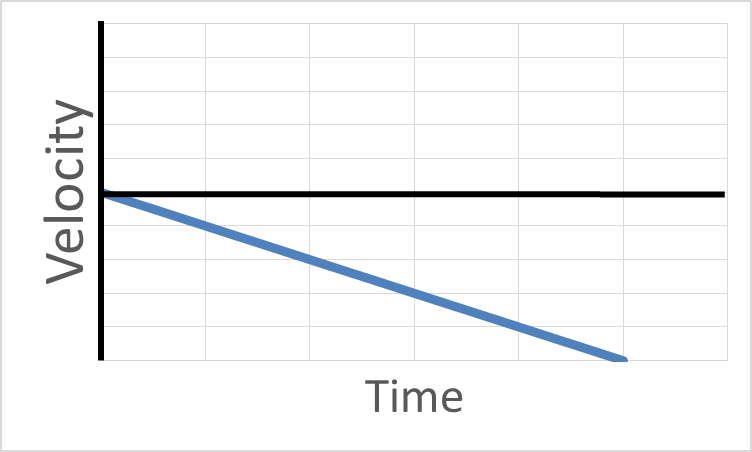
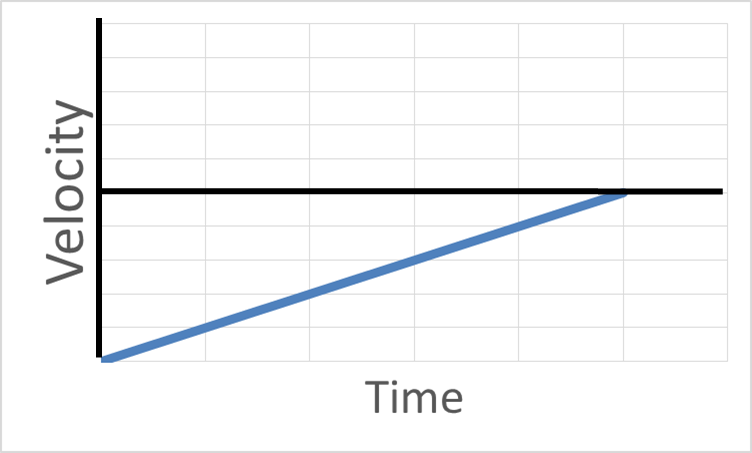
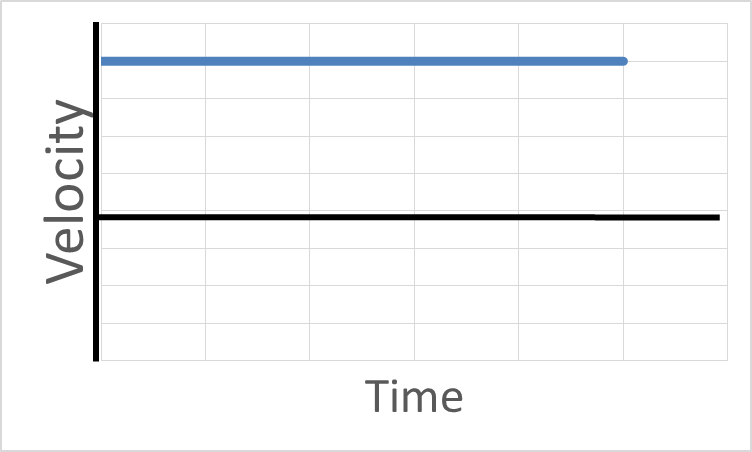
Click on a graph to see an explanation.

Acceleration Equations
Equations can help us find important information about an objects motion. These equations are accurate when acceleration is constant. To find the velocity after acceleration has happened:

initial velocity: initial velocity
acceleration: acceleration
time: time
To find the displacement after acceleration has happened:
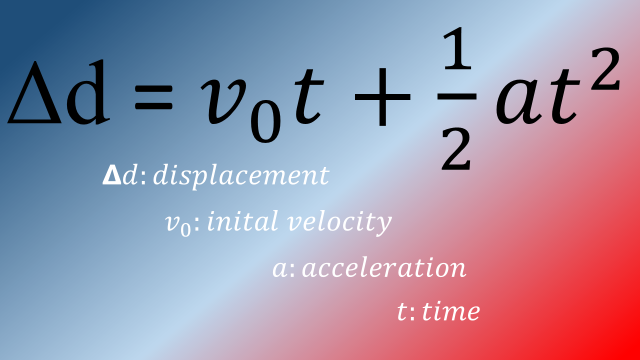
initial velocity: initial velocity
acceleration: acceleration
time: time
To find the new position after acceleration has happened:
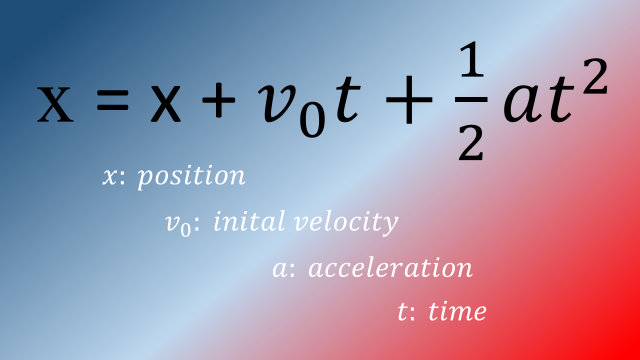
initial velocity: initial velocity
acceleration: acceleration
time: time
Here is an example of how these equations are used to find information about an object's motion after acceleration occurs. Click on the pictures to watch how to use each equation. Click on the 'Next Example' to go on to the next example:
Buppa Head starts at 0 m and accelerates with an acceleration of m/s2